

First, calculate the standard deviation, then plug that value into the SEM formula. Here are the steps you can use to calculate the standard error of the mean using a sample of five SAT test scores.
#How do you calculate standard error of the mean how to#
Related: How To Calculate Standard Deviation in 4 Steps (With Example) How to calculate SEM X̄ = the sample mean, find this value first The formula for sample standard deviation is expressed as: Note that σ is the Greek letter sigma and √ is the square root symbol. The formula for the standard error of the mean is expressed as: Inferential Statistics: Differences and Ways to Measure Standard error of the mean formula Standard deviation is the square root of the variance Standard error is the standard deviation divided by the square root of the sample size The degree to which people within the sample differ from the actual mean Measures how far the sample mean is likely to be from the actual population mean Standard error of the mean and standard deviation are both measures of variability used to summarize sets of data.Įstimates the variability across multiple samples of a populationĪn inferential statistic that can be estimatedĪ descriptive statistic that can be calculated Related: How To Calculate Standard Error in Excel (With Tips) Standard error of the mean vs. You can then use the standard error of the mean to determine how much the weight varies from the mean. However, if you look at the mean of the sample data, the samples will only vary by a few pounds. You can decrease standard error by increasing sample size.įor example, if you measure the weight of a large sample of men, their weights could range from 125 to over 300 pounds. A low standard error shows that sample means are closely distributed around the population mean, which means that your sample is representative of your population. Standard error functions are used to validate the accuracy of a sample of multiple samples by analyzing the deviations within the means.Ī high standard error shows that sample means are widely spread around the population mean, so your sample may not closely represent your population. Mean refers to the average of the numbers. In statistics, standard deviation is a measure of how spread out numbers are. It helps you estimate how well your sample data represents the whole population by measuring the accuracy with which the sample data represents a population using standard deviation.

The standard error of the mean (SEM) is used to determine the differences between more than one sample of data. In this article, we define standard error of the mean, explain how it varies from standard deviation and offer a formula to calculate it. Verifying the accuracy of your sample validates your clinical study and helps you make valid conclusions. –taken from comments by John W.If you’re gathering data for scientific or statistical purposes, the standard error of the mean can help you determine how closely a set of data represents that actual population. The standard error turns out to be an extremely important statistic, because it is used both to construct confidence intervals around estimates of population means (the confidence interval is the standard error times the critical value of t) and in significance testing. How good this estimate is depends on the shape of the original distribution of sampling units (the closer to normal the better) and on the sample size (the larger the sample the better). This estimate is derived by dividing the standard deviation by the square root of the sample size. In lieu of taking many samples one can estimate the standard error from a single sample. The standard deviation of this set of mean values is the standard error. We calculate the mean of each of these samples and now have a sample (usually called a sampling distribution) of means. Let’s say that instead of taking just one sample of 10 plant heights from a population of plant heights we take 100 separate samples of 10 plant heights.
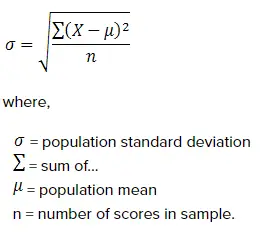
The standard error, on the other hand, is a measure of the variability of a set of means. The 5 cm can be thought of as a measure of the average of each individual plant height from the mean of the plant heights. We can say that our sample has a mean height of 10 cm and a standard deviation of 5 cm.

Let’s say we have a sample of 10 plant heights. The standard deviation is a measure of the variability of a single sample of observations. What is the difference between STANDARD DEVIATION and STANDARD ERROR?


 0 kommentar(er)
0 kommentar(er)
